Solving the closest-pair problem

Posts: 15
Comments: 31
Trackbacks: 0

<< Algorithmic Alley | Home | A faster method for solving the closest-pair problem >>

The first problem we’ll analyze comes from computational geometry, which is a very formal way of saying that we need to do some analysis on a graph. So, given a graph of points, like this:

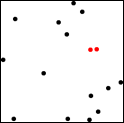
We’re going to analyze the list of points to decide which two are closest together. Eyeballing it, we can see that the closest two are the pair in red.

So how do we find the closest pair algorithmically? Easy –we’ll simply find every pair of points, sort them in order of distance, and take the mininum pair.

Oddly, the .Net framework doesn’t have any sort of Segment class, so first we’ll define our own:

public class Segment

    {
        public Segment(PointF p1, PointF p2)
        {
            P1 = p1;
            P2 = p2;
        }
 
        public readonly PointF P1;
        public readonly PointF P2;
 
        public float Length()
        {
            return (float)Math.Sqrt(LengthSquared());
        }
 
        public float LengthSquared()
        {
            return (P1.X - P2.X) * (P1.X - P2.X)
                + (P1.Y - P2.Y) * (P1.Y - P2.Y);
        }
 
        public override bool Equals(object obj)
        {
            var other = obj as Segment;
            if (other == null) return false;
 
            return P1 == other.P1 && P2 == other.P2;
        }
 
        public override string ToString()
        {
            return String.Format("{0} - {1}", P1, P2);
        } 
    }

And solve the problem.

    public class ClosestPointSolver
    {
        public Segment Closest_BruteForce(List<PointF> points)
        {
            int n = points.Count;
            var allPairs = Enumerable.Range(0, n - 1)
                .SelectMany(i => Enumerable.Range(i + 1, n - (i + 1))
                    .Select(j => new Segment(points[i], points[j])));
 
            return allPairs.OrderBy(seg => seg.LengthSquared())
                    .First();
        }
    }

Is this a good solution? Absolutely not. Looking at every single pair of points means that number of comparisons we have to do doubles every time we add another point. Going from 20 to 21 points still isn’t a big deal, but if you go from 100,000 to 100,001 points you’ll notice a significant difference. (It’s O(n²) in standard parlance, which I bet you know if you’re reading this, although I’ll probably cover it later in any case.)

So can we improve it? You bet. Next time.

(Image thanks to Wikimedia Commons http://commons.wikimedia.org/wiki/File:ClosestPair.png )