Ben Fulton
As is often the case, we’ll speed up the solver by using the divide-and-conquer method. We’ll split the graph down the middle, solve the problem for the left side, solve the problem for the right side, and we’ll be done!
How do we solve the problem for the left side? Easy! We’ll split the graph down the middle, solve the problem for the left side, solve the problem for the right side, and we’ll be done!
This technique is called recursion. The key thing to understand about recursion in general is that there has to be a stopping point. For example, a function to calculate a factorial might look something like this:
int Factorial(int i)
{
return Factorial(i - 1) * i;
}
But this function won’t work, because it will continually call itself over and over until the machine can’t handle it any more. So, we’ll just add a stopping point to say that the factorial value of 1 is, yes, 1. int Factorial(int i)
{
if (i == 1) return 1;
return Factorial(i - 1) * i;
}
When will we stop our algorithm? It's a pretty fair bet that if there are three points or less left to be analyzed, the brute-force method will work just as well as any other, so we'll use that as a limit. So, here's what we have so far:
Segment Closest_Recursive(List<PointF> points)
{
if (points.Count() < 4) return Closest_BruteForce(points);
int split = points.Count() / 2;
var ordered = points.OrderBy(point => point.X); // sort the points by their x value
var pointsOnLeft = ordered.Take(split).ToList(); // split into two groups, those to the
var pointsOnRight = ordered.Skip(split).ToList(); // left and those to the right
var leftMin = Closest_Recursive(pointsOnLeft);
var rightMin = Closest_Recursive(pointsOnRight);
if (leftMin.Length() < rightMin.Length())
return leftMin;
else
return rightMin;
}
But there’s a snag. Do you see it?
Suppose as we recurse along we end up drawing one of our lines like this:
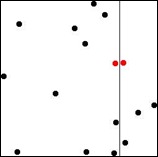
Now our closest pair is neither on the right or left. It crosses between the two. So it seems like we still have to examine each point to see if it’s closer to a point on the other side than it is to any points on its side.
But, we have some additional information to work with now. We know the distance between the two closest points that don’t cross the line. That means that if there are any crossing pairs that are closer, they will have to be at least that close to the line. Let’s find all the points on the right-hand side that are that close:
float minDist = Math.Min(leftMin.Length(), rightMin.Length());
var xDivider = pointsOnLeft.Last().X;
var closeY = pointsOnRight.TakeWhile(point => point.X - xDivider < minDist).OrderBy(point => point.Y);
It’s handy the points are sorted by X value – it allows us to stop our search once we get too far away from the line. And, note that closeY is sorted by the Y values now. This allows us to analyze only a small number of points on the right for each point on left. To finish off, we’ll take all the points on the left that are close to the line, and for each one, only examine the points on the right that are closer than minDist in the Y direction.
var crossingPairs = pointsOnLeft.SkipWhile(point => xDivider - point.X > minDist)
.SelectMany(p1 => closeY.SkipWhile(i => i.Y < p1.Y - minDist)
.TakeWhile(i => i.Y < p1.Y + minDist)
.Select(p2 => new Segment(p1, p2)));
And take the shortest distance out of everything.
return crossingPairs.Union(new[] { leftMin, rightMin })
.OrderBy(segment => segment.Length()).First();
Is it faster? Well, I posted some speed comparisons on RosettaCode. You can see there that for 10,000 points on the graph, this method ran in slightly more than a second. The brute-force method? Nearly two and a half minutes. Choosing the right algorithm can make all the difference in the world :)
Source code available here: http://github.com/benfulton/Algorithmic-Alley